Số nguyên tố là chuyên đề toán liên quan đến nhiều cấp học. Do đó, trong bài viết ngày hôm nay, hãy cùng dienmaybamien.com tổng hợp lại các kiến thức liên quan và một số dạng bài tập phổ biến về số nguyên tố nhé!

Số nguyên tố là gì?

Số nguyên tố là những số chỉ có 2 ước số là 1 và chính nó. Ví dụ:

• 5 là số nguyên tố vì cách duy nhất để viết chúng dưới dạng một tích đó là 1 x 5 hoặc 5 x 1, có một thừa số chính là số 5.
• 4 không phải số nguyên tố vì chúng là tích của nhiều số mà trong đó có hai số mà cả 2 số đều nhỏ hơn 4 (2 x 2, 1 x 4 hoặc 4 x 1). Khi đó, ta gọi 4 là hợp số.

Số nguyên tố là gì?

Số nguyên tố là những số nào?

Dưới đây là các số nguyên tố nhỏ hơn 100, mời bạn tham khảo: 

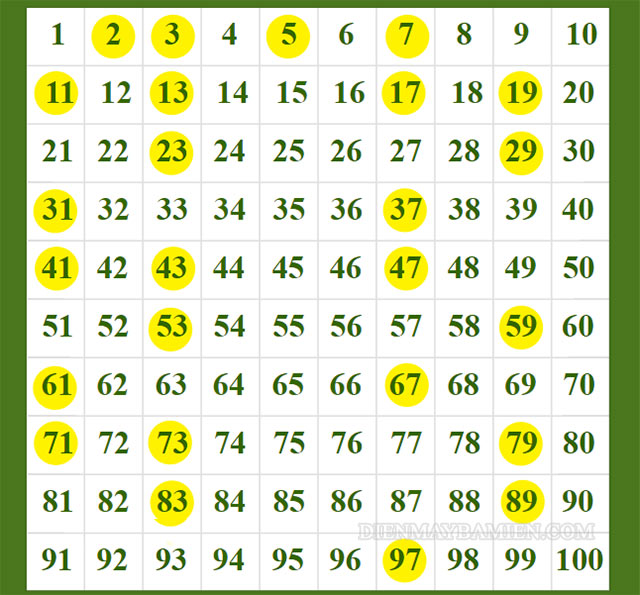
Bảng tổng hợp các số nguyên tố nhỏ hơn 100

Các tính chất cơ bản của một số nguyên tố

• Số 2 vừa là số nguyên tố nhỏ nhất, vừa là số nguyên tố chẵn duy nhất trong bảng số nguyên tố
• Số nguyên tố là vô hạn, không thể tập hợp được tất cả các số nguyên tố trong cùng một bảng
• Khi nhân 2 số nguyên tố với nhau, tích của chúng không thể là số chính phương
• Ước số tự nhiên nhỏ nhất (≠ 1) của một số được coi là số nguyên tố
• Ước số bé nhất (≠ 1) của một tập hợp số a bất kỳ sẽ là một số nguyên tố nếu chúng không vượt quá căn bậc 2 của a

3 cách tìm số nguyên tố cơ bản

Cách 1: Chia thử nghiệm

Với cách này, chúng ta chỉ cần chia số cần kiểm tra theo lý thuyết của số nguyên tố là được. Tuy nhiên, phương pháp này có thể mất nhiều thời gian và rất dễ xảy ra sai số trong quá trình thực hiện nên chúng không thường xuyên được sử dụng.

Cách 2: Lặp từng phần tử với bước nhảy 1

Với phương pháp sử dụng máy tính này, bạn chỉ cần áp dụng các bước sau :

• Bước 1: Nhập số cần kiểm tra vào n
• Bước 2: Sau khi kiểm tra, máy tính trả về kết quả n
• Bước 3: Lặp lại từ 2 đến n - 1, nếu trong khoảng này tồn tại số mà n chia hết thì kết luận n không phải số nguyên tố. Ngược lại, nếu không tồn tại số dương nào mà n chia hết thì n là số nguyên tố. 

Cách 3: Lặp từng phần tử với bước nhảy 2

Theo định nghĩa của số nguyên tố thì 2 là số nguyên tố nhỏ nhất, đồng thời là số nguyên tố chẵn duy nhất. Thế nên ta sẽ dễ dàng loại được số 2 ra khỏi vòng lặp. 

Khi đó, trong phần vòng lặp, bạn chỉ cần kiểm tra bằng những số lẻ. Phương pháp này tuy chưa tối ưu bằng cách 2 nhưng sẽ cho ra kết quả đúng hơn cách 1 rất nhiều.

Tìm số nguyên tố bằng casio

Bài tập vận dụng về số nguyên tố và hợp số

Bài tập 1: Cho n và 2n + 1 đều là số nguyên tố (n > 3). Hỏi 4n + 1 là hợp số hay số nguyên tố?

Lời giải:

Do n là một số nguyên tố lớn hơn 3 nên n không chia hết cho 3 → 4n không chia hết cho 3. (1)

Bên cạnh đó, do 2n + 1 là số nguyên tố lớn hơn 3 nên 2n + 1 không chia hết cho 3. → 2 x (2n + 1) không chia hết cho 3 → 4n +2 không chia hết cho 3. (2)

Mặt khác, trong 3 số tự nhiên liên tiếp 4n, 4n + 1, 4n + 2 sẽ có 1 số chia hết cho 3. (3)

Từ (1), (2) và (3), ta có: 4n + 1 chia hết cho 3, mà 4n + 1 > 3 → 4n + 1 là hợp số.

Bài tập 2: Cho n và n + 4 là 2 số nguyên số (n > 3). Hãy chứng minh rằng n + 8 là một hợp số.

Lời giải

Vì n là số nguyên tố lớn hơn 3 nên n = 3k + 1 hoặc n = 3k + 2. Từ đó, ta có 2 trường hợp:

• Trường hợp 1: nếu n = 3k + 2 thì n = 3k + 6 chia hết cho 3 → Loại
• Trường hợp 2: nếu n = 3k + 1 thì n + 7 = 3k + 8 không chia hết cho 3 → 2 x (n + 7) không chia hết cho 3 hay 2n + 14 không chia hết cho 3. Mà trong ba số tự nhiên liên tiếp sẽ có 1 số chia hết cho 3, suy ra: 2n + 16 chia hết cho 3 hoặc n + 8 chia hết cho 3 → n + 8 là một hợp số.

Bài tập 3: Hãy tìm 3 số lẻ liên tiếp đều là số nguyên tố

Lời giải

Giả sử, n, n + 2, n + 4 là 3 số lẻ liên tiếp đều là số nguyên tố, ta có:

• Nếu n = 3 thì n + 2 = 5 và n + 4 = 7 đều là số nguyên tố (thỏa mãn) (1)
• Nếu n > 3 thì n = 3k + 1 hoặc n = 3k + 2

Khi đó, với n = 3k + 1 thì n + 2 = 3k + 3 → chia hết cho 3 (loại) (2)

Với n = 3k + 2 thì n + 4 = 3k + 6 → chia hết cho 3 (loại) (3)

Vậy từ (1), (2), (3), ta có các số 3, 5, 7 là ba số liên tiếp đều là số nguyên tố

Bài tập 4: Tìm ba số nguyên tố dạng n , n + 10 , n + 20

Lời giải

Ta có: n, (n + 1) + 9, (n + 2) +18. Trong đó 3 số n, n + 1 và n + 2 luôn có 1 số chia hết cho 3 →  n, (n + 1) + 9, (n + 2) +18 luôn có một số chia hết cho 3.

Vậy nếu n = 3 → n, (n + 1) + 9, (n + 2) +18 ⇔ 3, 13, 23

Bài tập 5: Tìm số tự nhiên k để 29k là số nguyên tố? Tại sao 2 là số nguyên tố chẵn duy nhất trong các số nguyên tố?

Lời giải

1. Ta có 3 trường hợp sau:

Với k = 0 → 29k = 0 (< 2) → Loại

Với k = 1 thì 29k = 29 là số nguyên tố → Thỏa mãn

Với k > 1 thì 29k sẽ lớn hơn 29 và chia hết cho 29 → Loại

→ Vậy khi và chỉ khi k = 1 thì 29k mới là một số nguyên tố

1. 2 được coi là số nguyên tố chẵn duy nhất trong các số nguyên tố vì nếu có một số chẵn lớn hơn 2, chúng sẽ chia hết cho 2 và ước số của chúng ngoài 1 và chính nó thì còn có thêm ước số 2 → số tự nhiên chẵn lớn hơn 2 là hợp số.

Bài tập 6: Hãy tìm một số nguyên tố, sao cho số liền sau của nó cũng là một số nguyên tố

Lời giải

Ta biết, trong 2 số tự nhiên liên tiếp luôn bao gồm một số chẵn và một số lẻ. Bên cạnh đó, số nguyên tố chẵn bé nhất là 2, mà số liền kề với 2 là 3 cũng là một số nguyên tố.

→ Vậy số nguyên tố cần tìm là 2 

Bài tập 7: Hãy xét xem các số tự nhiên từ 1991 đến 2005, trong đó những số nào là số nguyên tố?

Lời giải

Đầu tiên, ta cần loại bỏ tất cả các số chẵn từ 1992 đến 2004 và loại bỏ các số chia hết cho 3 như 1995 và 2001. Ta còn các số 1991, 1993, 1997, 1999 và 2003. Trong đó số 1991 lại chia hết cho 11 → Loại.

Vậy, từ 1991 đến 2005 chỉ có 4 số nguyên tố đó là: 1993, 1997, 1999 và 2003.

Trên đây là toàn bộ thông tin cơ bản về số nguyên tố mà Điện máy Ba Miền tổng hợp được. Hy vọng qua bài viết trên, bạn đã hiểu được thế nào là một số nguyên tố, cách kiểm tra số nguyên tố bằng phương pháp bấm máy tính,... 

XEM THÊM:

• Cầu toàn là gì? Người cầu toàn có tốt không?
• Chân thành là gì? Chân thành hay trân thành là đúng chính tả?

Ngoài ra, đừng quên tham khảo các bài viết khác của chúng tôi tại website dienmaybamien.com để theo dõi và cập nhật được những kiến thức toán học hay ho, bổ ích khác nhé!