Đường trung tuyến là gì? Tính chất, công thức tính độ dài và bài tập vận dụng

Đường trung tuyến là nội dung quan trọng trong Toán hình học mà chúng ta được học ở cấp 2. Vậy đường trung tuyến là gì? Tính chất, công thức tính độ dài như nào? Hãy cùng chúng tôi tìm hiểu chi tiết về nội dung toán học này qua các thông tin trong bài nhé.

Đường trung tuyến là gì?

Đường trung tuyến của một đoạn thẳng chính là đường thẳng đi qua trung điểm của đoạn thẳng đó.

Đường trung tuyến của tam giác là gì? Đường trung tuyến của một tam giác chính là đoạn thẳng được nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác đều sẽ có ba đường trung tuyến ứng với 3 đỉnh.

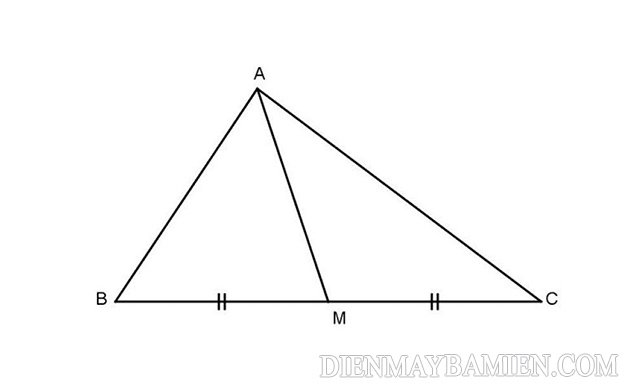
AM là đường trung tuyến tại đỉnh A trong tam giác ABC

Tính chất của đường trung tuyến

Sau khi đã hiểu rõ đường trung tuyến là đường gì ở bên trên, chúng ta sẽ cùng tìm hiểu chi tiết về tính chất của nó ở dưới đây:

Trong tam giác thường

Ba đường trung tuyến của tam giác sẽ cùng đi qua một điểm và điểm đó cách các đỉnh một khoảng bằng 2/3 độ dài của đường trung tuyến đi qua đỉnh ấy. Giao điểm của ba đường trung tuyến trong một tam giác thường được gọi là trọng tâm.

Gọi G là trọng tâm của tam giác ABC, các trung tuyến là AI, BM, CN thì chúng ta sẽ có biểu thức: AG/AI = BG/BM = CG/CN = 2/3

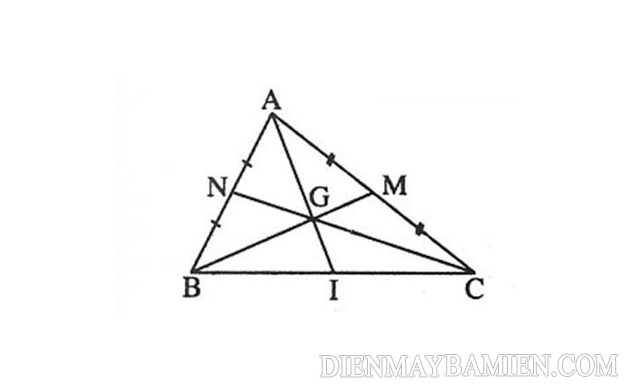
Các đường trung tuyến của tam giác giao nhau tại trọng tâm G

Trong tam giác vuông

Trong tam giác vuông, trung tuyến ứng với cạnh huyền sẽ có độ dài bằng 1/2 cạnh huyền.

Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa của cạnh đó thì tam giác ấy là tam giác vuông.

Đường trung tuyến của tam giác vuông có đầy đủ các tính chất của một đường trung tuyến trong tam giác thường.

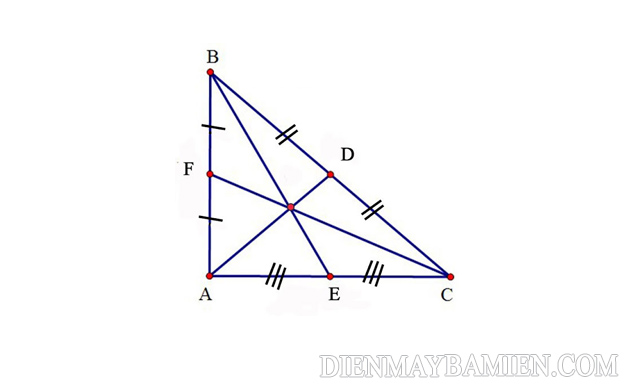
AD là đường trung tuyến của tam giác vuông ABC vuông tại A

ABC vuông có AD là đường trung tuyến ứng với cạnh huyền BC.

=> AD = BC/2 = DB = DC

Ngược lại, nếu đường trung tuyến AM =  BC/2 thì tam giác ABC vuông tại A.

Trong tam giác cân

Đường trung tuyến ứng với cạnh đáy sẽ vuông góc với cạnh đáy và chia tam giác thành 2 tam giác bằng nhau.

Cho tam giác ABC cân tại A, có đường trung tuyến AD ứng với cạnh BC 

=> AD ⊥ BC và ΔADB = ΔADC

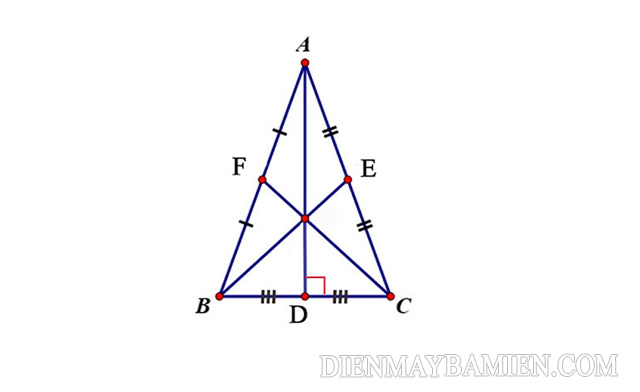
AD là đường trung tuyến tại đỉnh A của tam giác cân ABC 

Trong tam giác đều

Ba đường trung tuyến ứng với mỗi đỉnh trong tam giác đều sẽ chia tam giác đó thành 6 tam giác nhỏ có diện tích bằng nhau.

Trong tam giác đều, đường thẳng đi qua một đỉnh bất kỳ và trọng tâm của tam giác đó sẽ chia tam giác thành 2 tam giác có diện tích bằng nhau.

Cho tam giác ABC đều. G là trọng tâm của tam giác. E, F, G lần lượt là trung điểm của các cạnh AB, AC và BC.

=> ΔGAE = ΔGAF = ΔGCF = ΔGCD = ΔGBD = ΔGBE = ΔGEB = ΔGEA và SADB = SADC = SCEA = SCEB = SBFA = SBFC

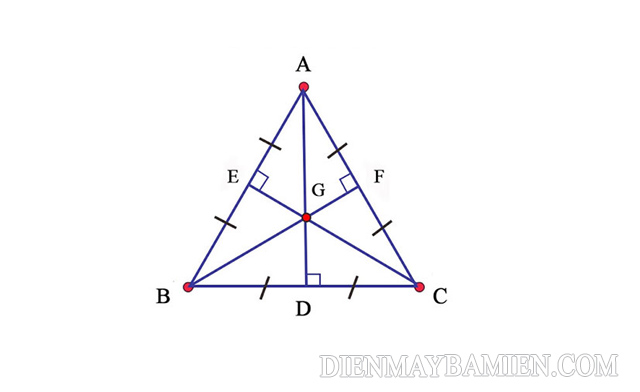
AD, BF, CE là các đường trung tuyến của tam giác đều ABC

Công thức tính độ dài của đường trung tuyến trong một tam giác

Độ dài đường trung tuyến trong một tam giác thường được tính thông qua độ dài các cạnh của tam giác và thường được tính bằng định lý apollonius. Cụ thể như sau:

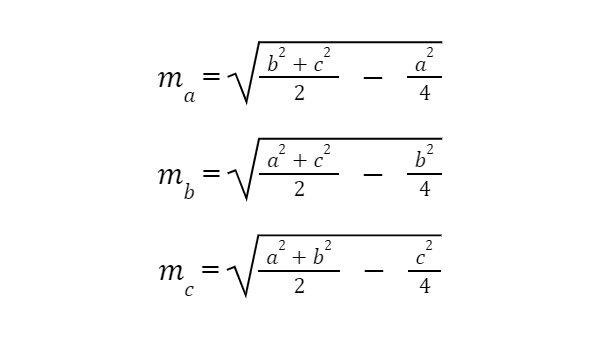
Trong đó:

• a, b, c là độ dài của các cạnh trong tam giác.
• ma, mb, mc là các đường trung tuyến đi qua các đỉnh của tam giác. 

Bài tập vận dụng về đường trung tuyến

Để củng cố kiến thức và ghi nhớ được lâu, các bạn hãy cùng chúng tôi làm bài tập vận dụng đường trung tuyến bên dưới đây nhé.

Bài tập 1: Cho hai đường thẳng x’x và y’y giao nhau ở O. Trên tia Ox lấy hai điểm A và B sao cho điểm A nằm giữa 2 điểm O và B và AB = 2OA. Trên y’y  lấy hai điểm L và M sao cho điểm O là trung điểm của đoạn thẳng LM. Nối điểm B với L, B với M. Gọi P là trung điểm của đoạn thẳng MB và Q là trung điểm của đoạn thẳng LB. Hãy chứng minh các đoạn thẳng LP và MQ đi qua điểm A.

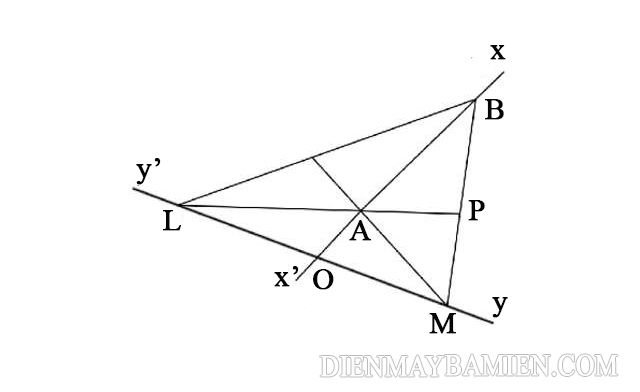
Hình minh họa bài tập 1

Cách giải

Ta có điểm O là trung điểm của đoạn LM (theo giả thiết)

=> BO là đường trung tuyến của tam giác BLM (1)

Mặt khác lại có BO = BA + AO vì điểm A nằm giữa O, B

<=> BO = 2 AO + AO = 3AO vì AB = 2AO (theo giả thiết)

=> AO =  BO/3 hay BA= 2BO/3 (2)

Từ (1) và (2) => A chính là trọng tâm của tam giác BLM (theo tính chất của trọng tâm tam giác)

Ta có LP và MQ là các đường trung tuyến của tam giác BLM 

=> Các đoạn thẳng LP và MQ đều đi qua điểm A (theo tính chất của ba đường trung tuyến) 

Bài tập 2: Cho tam giác ABC có BM và CN là hai đường trung tuyến cắt nhau tại điểm G. Kéo dài BM lấy điểm E sao cho ME = MG. Kéo dài đoạn thẳng CN lấy điểm F sao cho NF = NG. Hãy chứng minh:

1.  EF = BC
2. Đường thẳng AG đi qua trung điểm của cạnh BC.

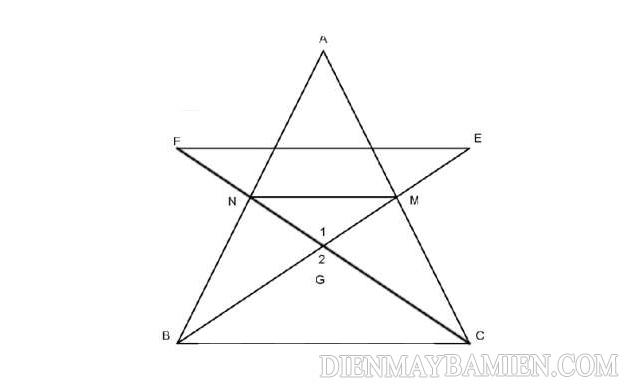
Hình minh hoạ bài tập 2

Cách giải

a) Ta có BM và CN là hai đường trung tuyến giao nhau tại G nên G chính là trọng tâm của tam giác ABC.

=> GC = 2GN

mà FG = 2GN nên => GC = GF

Tương tự BG = GE và góc G1 = góc G2

=> tam giác BGC = tam giác EGF (c.g.c)

=> BC = EF

b) G là trọng tâm của tam giác ABC nên AG chính là đường trung tuyến thứ ba trong tam giác ABC => AG đi qua trung điểm của cạnh BC. 

XEM THÊM:

• 25251325 là gì? 1325 là gì? Nguồn gốc của con số
• Số nguyên tố là gì? Gồm những số nào? Tính chất

Bên trên là các thông tin chúng tôi chia sẻ cho các bạn về đường trung tuyến là gì? Tính chất, công thức tính độ dài và bài tập vận dụng. Hy vọng bài viết sẽ giúp các bạn củng cố được kiến thức và đạt được điểm cao trong học tập.